Artikel
Oleh : Drs. Dylmoon Hidayat, M.S., M.A., Ph.D
Banyak orang berpendapat bahwa belajar Matematika atau sain lainnya tidak perlu, bahkan tidak dapat disangkut-pautkan dengan iman Kristen. Sebenarnya, pendapat demikian menunjukkan hidup dalam dualitas kehidupan antara dunia sekuler dan keimanan. Hidup dalam dualitas kehidupan tidaklah nyaman, seperti orang yang tidak mempunyai pendirian yang sering kebingungan dalam menjawab suatu pertanyaan hendak dijawab secara sekuler atau secara iman.
Bagaimana melalui iman Kristen orang dapat memandang Matematika sebagai bagian yang utuh dari ciptaan Allah sehingga tidak terjadi dualitas dalam kehidupannya? Untuk menjawab pertanyaan ini, dibutuhkan empat hal dasar cara pandang yang dapat menjadikan Matematika sebagai suatu kesatuan di dalam dunia sain dan dunia kekristenan (iman Kristen). Cara pandang tersebut adalah pertama, sebagai alat untuk mengagumi ciptaan Allah, kedua dapat digunakan untuk mengenali sifat dan pekerjaan Allah yang tertulis dalam Alkitab, ketiga menjadi dasar untuk membangun ilmu pengetahuan yang walaupun terbatas namun berguna untuk melaksakan Mandat Budaya, dan yang keempat menerapkannya dalam kehidupan sehari-hari dengan memberikan makna sebagai pedoman hidup dalam rangkaian melaksanakan Amanat Agung. Tulisan ini menjelaskan bagian yang kedua dari keempat cara pandang matematika melalui iman Kristen. Tulisan pertama telah diterbitkan pada koran yang sama tanggal 16 Januari 2025. Nantikan penjelasan dua cara pandang lainnya pada tulisan yang akan datang.
Dalam Kitab Perjanjian Lama tertulis Firman Allah kepada Abraham: Lalu TUHAN membawa Abram ke luar serta berfirman: “Coba lihat ke langit, hitunglah bintang-bintang, jika engkau dapat menghitungnya”. Maka firmanNya kepadanya: “Demikianlah banyaknya nanti keturunanmu”. (Kej 15:5). Ayat ini mengenalkan konsep berhitung mula-mula yang menjadi dasar pengembangan matematika mulai dari yang dasar seperti Aritmetika sampai pada yang tingkat tinggi seperti Analisis Real. Adakah cara menghitung Bintang di langit? Bagaimana orang dapat memahami keterterhitungan dan ketidak-terhitungan dari banyaknya suatu benda? Apakah tak terhitung sama dengan tak terhingga?
Manusia mempunyai 1 mulut, 2 mata, 3 dimensi badan (panjang, lebar, dan tinggi), 5 panca indera (peraba, penglihat, pendengar, pencium, dan pengecap), 10 jari tangan, dan seterusnya. Itu semua adalah contoh-contoh dari himpunan yang terhitung namun berhingga golongan sedikit. Banyaknya rambut yang tumbuh di kepala manusia adalah terhitung dan berhingga tetapi banyak sekali.
Berhitung adalah cara memasangkan himpunan benda dengan himpunan bagian dari bilangan asli.
Contoh: menghitung himpunan abjad Bahasa Indonesia= {a, b, c, …, x,y,z}
Untuk himpunan benda-benda yang banyaknya k buah, jumlah anggota himpunan itu disebut berhingga, artinya ada himpunan bagian dari k bilangan asli pertama yang dapat dipasangkan dengan himpunan berhingga tersebut. Himpunan benda-benda yang banyaknya tak berhingga dihitung dengan cara memasangkan himpunan tersebut dengan himpunan bilangan Asli N= {1,2,3, …}. Himpunan benda disebut terhitung jika dapat ditemukan pemasangan antara himpunan benda tersebut dengan himpunan bagian bilangan asli. Jadi himpunan bilangan Asli itu sendiri adalah tak berhingga dan terhitung. Himpunan bilangan genap = {2, 4, 6, 8, . . .} adalah terhitung sebab dapat dipasangkan dengan himpunan bilangan asli, sebagai berikut:
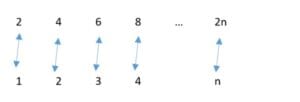
Himpunan bilangan pecahan Q= {m/ n: m, n bilangan Asli} adalah terhitung juga, walupun perlu teknik khusus cara memasangkan himpunan bilangan pecah Q dengan himpunan bilangan asli N. Jadi himpunan benda-benda terhitung dapat berhingga atau tak berhingga. Adakah himpunan benda-benda yang tak terhitung? Kalau ada, pastilah banyaknya “melebihi” himpunan terhitung yang tak hingga. Contoh himpunan yang tak terhitung adalah himpunan bilangan real antara 0 dan 1, yang disimbolkan dengan . Telah dibuktikan oleh seorang matematikawan bernama Cantor bahwa tidak ada cara apapun yang dapat memasangkan himpunan [0,1] dengan himpunan bilangan asli N. Jadi himpunan benda-benda yang tak terhitung adalah “jauh lebih banyak” dari pada himpunan yang terhitung.
Ketakhinggaan menjadi suatu konsep yang sangat membingungkan bagi sebagian besar orang. Fakta bahwa ketakhinggan pada himpunan bilangan Asli jauh lebih kecil dari ketahinggaan himpunan bilangan real [0,1] menginspirasi adanya dua jenis ketakhinggaan yang dapat dibandingkan. Dengan menggunakan lambang 
sebagai simbol tak hingga, maka dapat ditulis 
, di mana 
adalah ketakhinggaan pada himpunan bilangan Asli dan 
adalah ketakhinggaan pada himpunan bilangan real [0,1]. Dapat dicari pula suatu himpunan berukuran lebih besar dari himpunan bilangan real, sehingga dapat dibuktikan bahwa ada “banyak jenis” ketakhinggaan yang dapat diurutkan:
dan seterusnya.
Tertulis dalam Mazmur 147:5 “Besarlah Tuhan kita dan berlimpah kekuatan, kebijaksanaan-Nya tak terhingga. Jadi, simbol ketakhinggaan mana yang tepat menggambarkan banyaknya kebijaksanaan Allah yang tak terhingga itu? Yang jelas bukan , atau jenis apapun yang dapat didefinisikan oleh logika manusia. Manusia hanya dapat memahami dan memanfaatkan saja. Walaupun dapat dipahami adanya berbagai macam ketakhinggaan yang dapat diurutkan dari yang kecil tapi matematika tidak dapat menentukan apakah ada ketakhinggaan yang paling besar atau tidak. Jika ada, maka tentulah ketakhinggaan yang paling besar ini yang dimaksud dalam Mazmur 147: 5. Halleluya.
Terpujilah Allah!
Penulis : Drs. Dylmoon Hidayat, M.S., M.A., Ph.D Dosen Universitas Pelita Harapan